Проекция вектора

 

Вектора нам необходимы, но работать с ними непросто. Как разорвать это противоречие?

Надо преобразовать вектор к форме, которая более понятна и удобна в обращении. Такими привычными величинами являются скалярные величины. Вектор, превращенный в скаляр, называется проекцией.

Необходимо учесть, что проекция вектора определяется на ось координат. Таким образом, перед тем, как проецировать, необходимо ввести систему координат. На уроках математики мы систему координат изображали в виде осей Oxy. Получается, что оси две, а значит и проекций будет две у одного вектора: сколько осей, столько и проекций может быть. А если на чуть-чуть вспомнить, что мы живем в трехмерном мире, то становится ясно, что у вектора может быть и три проекции.

Раз вспомнили о математике, то надо сделать еще одно замечание. Оси координат мы рисуем всегда одну строго вверх, другую – перпендикулярно ей, то есть горизонтально. Но это не обязательно так . Ось может располагаться так, как вам пожелается, но главное, чтобы оси были взаимно перпендикулярны. Последнее обязательно.

Довольно нудной и сухой математики. Займемся делом. Мы собрались проецировать вектора.

С чего начать? Определяем ось, на которую проецируем. Пусть это будет ось Ох (оригинально, не правда ли). Из начала вектора опускаем перпендикуляр на ось: проводим прямую через начало отрезка перпендикулярно оси Ох до пересечения с ней. Получили проекцию начала вектора. Эта точка (проекция точки – точка) на рисунке названа X₀.

Кто-то скажет, что это координата Х начала вектора. В принципе, этот кто-то будет прав. Но тогда вспомним, что координата у нас всегда ассоциируется с числом. А что означает это число и откуда оно берется? Об этом кто-то обычно не помнит или не знает. А все просто: это число определяет расстояние от проекции точки до начала отсчета. На нашем рисунке числовое значение координаты X₀ является длиной зеленого отрезка.

Не отвлекаемся, возвращаемся к нашим проекциям. Те же операции выполняем для конца вектора. Получаем координату X, значение которой равно длине синего отрезка.

Проекцией вектора будет длина красного отрезка, то есть расстояние между координатами начала и конца вектора. Красный отрезок и будет отображением векторной величины в виде скалярной. Обозначается проекция той же буквой, что и вектор ( в нашем случае S). Но есть и различие. У самого вектора над головой висит стрелка . Проекция – не вектор, она потеряла направление, став скаляром. Поэтому обозначение проекции лишили стрелки, но внизу добавили значок оси, на которую спроецировали S_X.

Вектор и его проекция – это две большие разницы. Они отличаются так же как сам человек (вектор) и его тень.

Все, что мы проделали на ось Ох, можно выполнить и на ось Оу. При этом получится проекция вектора S на ось Оу (красный отрезок вдоль оси Оу, обозначенный S_Y)

Обратите внимание, что длины вектора и его проекций различны, да и длины проекций тоже различаются между собой. Это нормально: длина тени не всегда равна росту человека (пример так себе, так как тень может быть «выше» человека, а проекция никогда не будет длиннее вектора).

Длину проекции можно легко определить. Смотрите на рисунок: из длины синего отрезка убираем длину зеленого. Математически выражаясь, вычитаем. Получается довольно простые вычисления.

Теперь о главном. Вектор нам нужен, чтобы отображать величины с направлением, а у скалярной проекции направления нет. Как она отобразит направление вектора? Очень легко: у скалярных величин есть знак.

Если от проекции начала вектора к проекции конца мы движемся по направлению оси, то числовое значение проекции со знаком плюс, положительная проекция. А если такое же движение против направления оси, то значение проекции с минусом, отрицательное.

Для вектора на левом рисунке проекция на ось Ох положительная, а для вектора на правом рисунке – отрицательная. Мой любимый ученик Кто-то может сказать и так: «Если вектор «смотрит» в ту же сторону, что и ось, то проекция положительная, а если вектор и ось направлены в разные стороны, то проекция отрицательная». Можно и так, но… не красиво.

Формулы, написанные выше, для расчета длин проекций тоже дают знак проекции, но для этого нельзя переставлять местами значения конечной координаты и начальной. Менять их местами запрещено, иначе результат будет неправильным. Из конца вычитаем начало.

Теперь практика.

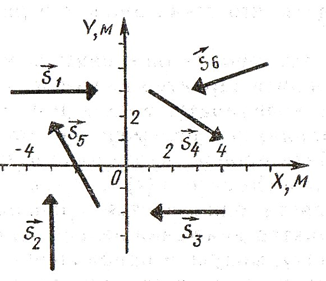
Определите ка у каких векторов на ось Ох положительная проекция, а у каких отрицательная.

(правильно, положительные проекции у векторов 1 и 4, отрицательные у 3 и 5, а вот у второго просто ноль)

Определите величины проекций векторов на ось Ох.

(Опять правильно! S_1x=4, S_2x=0, S_3x=-3, S_4x=3, S_5x=-2)

А теперь тоже самое для оси Оу, но без подсказок. Удачи.